[♀]Matemática na Veia 2007-2016 O Blog do Estudante Inteligente
Dois números binomiais são complementares se apresentam o mesmo numerador e se a soma de suas classes for igual a esse numerador.
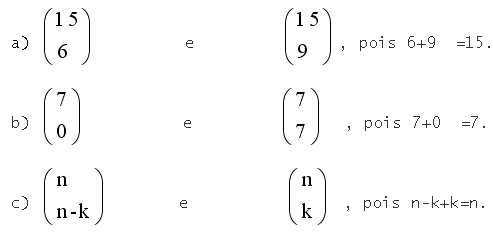
Podemos demonstrar que dois binomiais complementares são iguais. Assim:

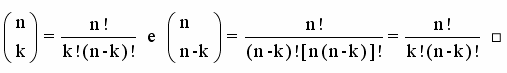
Por exemplo, observe os seguintes binomiais complementares
 dados no exemplo “a” :
dados no exemplo “a” :
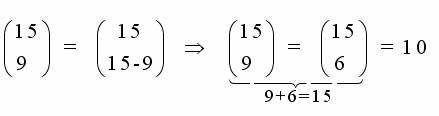
Como conseqüência dessa propriedade, temos:

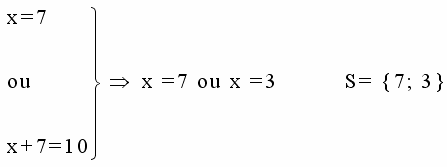


2- Gabarito
Em análise combinatória você tem as seguintes conteúdos disponíveis:
Observação:
- Após terminar seus downloads, passe um antivírus antes de abrir seu arquivo.
- Crie um ponto de restauração no Windows, antes de instalar qualquer programa, ou arquivo.
REFERÊNCIAS:
BACHX, A. de; POPPE, L. M. B.; TAVARES; RAYMUNDO N. O. – Prelúdio à Análise Combinatória. Companhia Editora Nacional. 1975
CARVALHO, P. C. P; LIMA, E. L.; MORGADO, A. C; WAGNER, E. – A Matemática do Ensino Médio. Vol. 2. Coleção do Professor de Matemática. Sociedade Brasileira de Matemática. 1998
CARVALHO, J. B. P; CARVALHO, P. C. P; FERNANDEZ, P; MORGADO, A. C de O. – Análise Combinatória e Probabilidade. Coleção do Professor de Matemática.
 Sobre a Autor:
Sobre a Autor:











Estou precisando de uma ajuda para resolver a seguinte questão (x 2)lê-se binomial de x sobre 2+ (x 3)binomial de x sobre 3=35 qual o valor de x.
ResponderExcluirEstou precisando de uma ajuda para resolver a seguinte questão (x 2)lê-se binomial de x sobre 2+ (x 3)binomial de x sobre 3=35 qual o valor de x.
ResponderExcluirE o teu nome (anonimo)?
Tem que abrir esta equação.
|x|
|2| = Cx,2= x!/2!(x-2)!
|x|
|3| = Cx,3= x!/3!(x-3)!
x!/2!(x-2)! + x!/3!(x-3)! =35
x(x-1)(x-2)! / 2!(x-2)! + x (x-1)(x-2)(x-3)! /3!(x-3)! = 35
simplificando
x(x-1)/2! +x (x-1)(x-2) /3! = 35
x(x-1)/2 +x (x-1)(x-2) /6 = 35
x²-x /2 +(x²-x)(x-2) /6 = 35
Bom! Melhor que isso só se vier uma GELADA acompanhado!
Um abraço!!!!
Olá como obteve na questão 1 a)19 sobre 22.
ResponderExcluir